Un cycliste effectue cinq tours de piste en 2 minutes 40 secondes. Sachant qu’à chaque tour, il a mis une seconde de plus qu’au précédent, déterminer le temps mis pour chaque tour. On donnera une résolution à l’aide d’une suite ou une résolution arithmétique.

Résolution à l’aide d’une suite (pour un élève de lycée)

Soit (U_n) la suite de terme initial U₀ sur l’ensemble des entiers naturels N.

Posons U₀=t et 2 minutes 40 secondes = 2*60+40=120+40=160

Nous avons alors U₁=t+1 ;

Puis U₂=t+2 ;

Et donc de manière générale, U_n=t+n.

Or, l’expression du terme général d’une suite arithmétique s’écrit :

U_n=U₀+n*r (avec r ∈ N).

Ainsi, il est facile de conclure que (U_n) est arithmétique de premier terme U₀=t et de raison 1.

La somme d’une suite arithmétique des cinq premiers termes s’écrit :

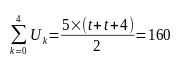
Cela revient à résoudre une équation du premier degré :

320=10*t+20

t=30

Le cycliste met donc 30 secondes au premier tour, puis 31, 32, 33 et 34 secondes.

Vérification : 30+31+32+33+34=160

Résolution arithmétique (pour un élève de collège avec mise en équation)

On sait que le cycliste effectue 5 tours en 160 secondes.

Soit t le temps qu’il met au premier tour, au second il mettra une seconde de plus, le temps au tour s’écrit alors t+1.

Donc nous pouvons poser t+t+1+t+2+t+3+t+4=160

5t+10=160

<=> 5t=150

<=> t=150/5

<=> t=30

Vérification : 30+31+32+33+34=160

Ce résultat corrobore le précédent.

Nous voyons que les méthodes différent (même si elles sont sensiblement identiques). Toutefois, il est opportun d’observer que pour arriver à une solution il n’y a pas forcément qu’un seul chemin.

Tous les chemins mènent à Rome.

« Mille viae ducunt homines per saecula Romam Qui Dominum toto quaerere corde volunt. » Version latine

« Mille routes conduisent depuis des siècles à Rome les hommes qui désirent rechercher le Seigneur de tout leur cœur. » Version Française