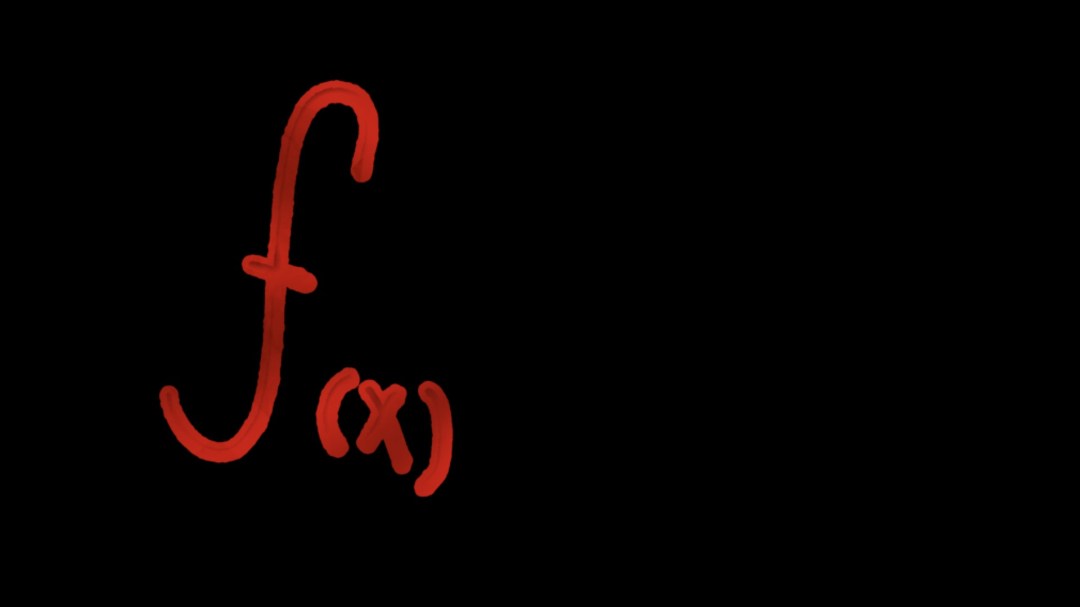Tout ce que vous avez voulu savoir au sujet des fonctions !

Introduction :

Présentation du sujet : Les fonctions

Les fonctions sont un concept fondamental en mathématiques, largement utilisé dans de nombreuses disciplines scientifiques et techniques. Elles permettent de modéliser des relations entre différentes variables et de prévoir des comportements futurs. Comprendre les fonctions est donc essentiel pour résoudre des problèmes pratiques et théoriques.

Importance des fonctions dans les mathématiques et dans la vie quotidienne

Les fonctions sont importantes en mathématiques car elles permettent de décrire des relations entre différentes variables, comme le temps et la distance, la température et la pression, ou le revenu et le niveau d’éducation. Elles sont utilisées dans de nombreux domaines scientifiques, de l’économie à la physique, pour modéliser des phénomènes complexes. Dans la vie quotidienne, les fonctions sont également omniprésentes. Elles permettent de prédire des tendances économiques, de concevoir des systèmes de communication, de modéliser des comportements humains, de résoudre des problèmes d’ingénierie, et bien plus encore. Comprendre les fonctions est donc essentiel pour réussir dans de nombreuses carrières et pour prendre des décisions éclairées dans de nombreux domaines de la vie.

Objectif de l’article : Fournir une compréhension complète des fonctions

L’objectif de cet article est de fournir une compréhension complète des fonctions, en expliquant leur définition, leur représentation graphique, ainsi que leur domaine et leur image. Nous visons à aider les lecteurs à mieux comprendre le concept de fonction, à savoir comment tracer le graphique d’une fonction, et comment trouver son domaine et son image. En fournissant une explication détaillée de ces sujets clés, nous espérons donner aux lecteurs les connaissances et les outils nécessaires pour résoudre des problèmes pratiques et théoriques, ainsi que pour approfondir leur compréhension des mathématiques.

Partie 1 : Définition des fonctions

Explication de ce qu’est une fonction

Une fonction est un concept mathématique fondamental qui décrit une relation entre deux ensembles de données : le domaine et l’image. En termes simples, une fonction prend un nombre ou une valeur en entrée et produit un résultat en sortie, qui dépend de la règle définie par la fonction. Par exemple, une fonction peut être utilisée pour décrire la relation entre la température et la pression dans un gaz, entre le temps et la distance parcourue par un objet, ou entre le revenu et le niveau d’éducation. Les fonctions sont généralement représentées sous forme d’équations, de tableaux ou de graphiques, et sont utilisées pour résoudre des problèmes pratiques et théoriques dans de nombreux domaines scientifiques et techniques.

Une fonction est aussi une relation univoque entre deux ensembles, appelés le domaine et l’image. Elle associe à chaque élément du domaine un unique élément de l’image, conformément à une règle bien définie. Formellement, une fonction f est définie par un ensemble de paires ordonnées (x,y), où x est un élément du domaine et y est un élément de l’image, tels que chaque élément x dans le domaine soit associé à un et un seul élément y dans l’image. Cette relation est souvent notée par l’équation f(x) = y, où x est l’entrée (ou l’argument) de la fonction, et y est la sortie (ou la valeur) de la fonction. Les fonctions sont utilisées pour modéliser une variété de phénomènes mathématiques et physiques, et sont représentées graphiquement par des courbes et des surfaces dans un système de coordonnées.

Les différents types de fonctions (linéaire, quadratique, exponentielle, etc.)

1. Les fonctions linéaires: Les fonctions linéaires sont des fonctions de la forme f(x) = ax + b, où a et b sont des constantes réelles. Ces fonctions sont caractérisées par une droite qui passe par l’origine et dont la pente est a. Les fonctions linéaires sont couramment utilisées pour modéliser des relations proportionnelles entre deux variables.
2. Les fonctions quadratiques: Les fonctions quadratiques sont des fonctions de la forme f(x) = ax² + bx + c, où a, b et c sont des constantes réelles. Ces fonctions sont caractérisées par une courbe en forme de parabole, qui peut être orientée vers le haut ou vers le bas. Les fonctions quadratiques sont utilisées pour modéliser une variété de phénomènes physiques et mathématiques, tels que le mouvement d’un objet en chute libre ou la forme d’une sphère.
3. Les fonctions exponentielles: Les fonctions exponentielles sont des fonctions de la forme f(x) = a^x, où a est une constante réelle. Ces fonctions sont caractérisées par une courbe en forme de croissance exponentielle, qui augmente de manière exponentielle avec l’entrée x. Les fonctions exponentielles sont utilisées pour modéliser des phénomènes de croissance, tels que la population d’une ville ou le taux d’infection dans une épidémie.
4. Les fonctions logarithmiques: Les fonctions logarithmiques sont des fonctions de la forme f(x) = log_a(x), où a est une constante réelle. Ces fonctions sont utilisées pour inverser les fonctions exponentielles, c’est-à-dire pour trouver l’entrée x correspondante à une certaine sortie y. Les fonctions logarithmiques sont couramment utilisées pour mesurer des quantités qui varient de manière exponentielle, telles que les niveaux sonores ou les niveaux de pH.
5. Les fonctions trigonométriques: Les fonctions trigonométriques sont des fonctions qui décrivent les relations entre les angles et les longueurs des côtés dans un triangle. Les fonctions trigonométriques les plus couramment utilisées sont le sinus, le cosinus et la tangente, qui sont utilisées pour résoudre des problèmes de géométrie et de trigonométrie.

Chacun de ces types de fonctions a des propriétés et des caractéristiques uniques qui les rendent utiles pour modéliser différents types de phénomènes mathématiques et physiques.

La notation utilisée pour représenter une fonction

La notation utilisée pour représenter une fonction est généralement de la forme f(x) = y, où f est le nom de la fonction, x est l’entrée (ou l’argument) de la fonction, et y est la sortie (ou la valeur) de la fonction. Le nom de la fonction peut être n’importe quoi, tant qu’il est clair et distinctif. Par exemple, une fonction qui calcule le carré d’un nombre peut être appelée f(x) = x^2.

La notation f(x) est souvent utilisée pour représenter une fonction continue, c’est-à-dire une fonction qui peut prendre n’importe quelle valeur dans un intervalle continu. Pour les fonctions discrètes, c’est-à-dire les fonctions qui prennent des valeurs entières ou discrètes, une notation différente peut être utilisée. Par exemple, une fonction qui calcule le nombre de personnes dans une salle peut être notée par N(t), où t représente le temps et N est le nombre de personnes.

La notation f(x) peut également être utilisée pour représenter des fonctions de plusieurs variables, c’est-à-dire des fonctions qui dépendent de plusieurs entrées. Dans ce cas, la notation devient f(x1, x2, …, xn) = y, où x1, x2, …, xn sont les entrées de la fonction et y est la sortie.

Il existe également d’autres notations pour représenter les fonctions, telles que la notation de Leibniz (dy/dx) pour les dérivées, ou la notation intégrale (∫) pour les intégrales. Cependant, la notation f(x) reste la notation la plus couramment utilisée pour représenter les fonctions dans les mathématiques et les sciences.

Partie 2 : Représentation graphique des fonctions

Introduction à la représentation graphique des fonctions

La représentation graphique des fonctions est un outil important en mathématiques pour visualiser les relations entre les entrées et les sorties d’une fonction. Elle permet de comprendre plus facilement les propriétés d’une fonction, telles que son domaine, son image, sa parité, sa périodicité, etc.

Pour représenter graphiquement une fonction f(x), on utilise un plan cartésien où l’axe des abscisses représente les entrées de la fonction (x), et l’axe des ordonnées représente les sorties de la fonction (y = f(x)). On trace ensuite la courbe représentative de la fonction en reliant les points de coordonnées (x, f(x)) pour chaque valeur de x dans le domaine de la fonction.

Par exemple, la représentation graphique de la fonction linéaire f(x) = ax + b est une droite dont la pente est a et l’ordonnée à l’origine est b. La représentation graphique de la fonction quadratique f(x) = ax^2 + bx + c est une parabole dont la forme dépend des coefficients a, b et c.

La représentation graphique des fonctions permet également de visualiser les intersections entre différentes fonctions, les valeurs maximales et minimales, les asymptotes, etc. Elle est donc un outil précieux pour l’analyse des fonctions et leur utilisation dans des applications pratiques, telles que la modélisation de phénomènes naturels ou économiques.

Comment tracer le graphique d’une fonction à partir de son équation

Pour tracer le graphique d’une fonction à partir de son équation, il faut d’abord déterminer le domaine de la fonction, c’est-à-dire l’ensemble des valeurs pour lesquelles la fonction est définie. Ensuite, il faut calculer les valeurs de la fonction pour différentes valeurs de x dans son domaine, afin de pouvoir tracer la courbe représentative de la fonction.

Voici les étapes à suivre pour tracer le graphique d’une fonction à partir de son équation :

1. Déterminer le domaine de la fonction en résolvant les éventuelles contraintes sur x, telles que les valeurs interdites ou les asymptotes verticales.
2. Identifier les points d’intersection de la fonction avec les axes des abscisses et des ordonnées, en résolvant f(x) = 0 ou en calculant f(0) ou f(c) pour une valeur appropriée de c.
3. Calculer les valeurs de la fonction pour différentes valeurs de x dans son domaine, en utilisant les règles algébriques appropriées pour simplifier l’expression de la fonction. On peut également utiliser une table de valeurs ou une calculatrice pour obtenir des approximations numériques.
4. Tracer la courbe représentative de la fonction en reliant les points de coordonnées (x, f(x)) pour chaque valeur de x dans le domaine de la fonction. On peut également utiliser des outils graphiques, tels que les asymptotes, les points d’inflexion, les tangentes, etc., pour améliorer la précision du tracé.

Il est important de noter que le tracé du graphique d’une fonction peut être influencé par les propriétés de la fonction, telles que sa parité, sa périodicité, sa continuité, etc. Il est donc important de bien comprendre ces propriétés avant de tracer le graphique d’une fonction.

Les différents types de courbes que l’on peut obtenir en fonction du type de fonction

Il existe plusieurs types de courbes que l’on peut obtenir en fonction du type de fonction :

• Les fonctions linéaires : ces fonctions ont une courbe représentative qui est une droite, avec une pente constante. La forme de la courbe dépend de la valeur de la pente et de l’ordonnée à l’origine.

Exemple de fonction linéaire : y = 2x + 1

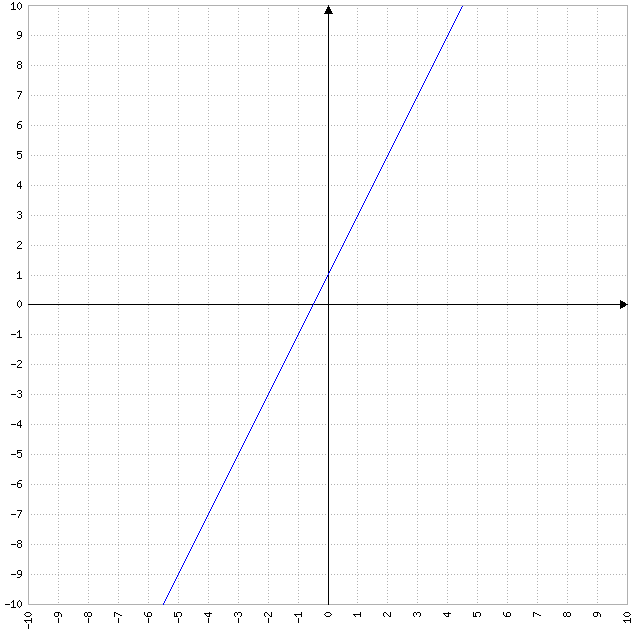
• Les fonctions quadratiques : ces fonctions ont une courbe représentative qui est une parabole, avec une forme qui dépend des coefficients de la fonction. La parabole peut s’ouvrir vers le haut ou vers le bas, être symétrique ou non, etc.

Exemple de fonction linéaire : y = x²-3x+2

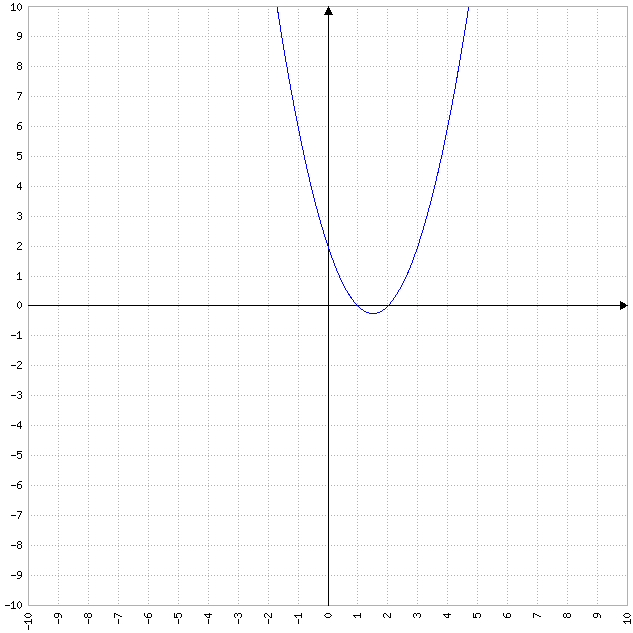
• Les fonctions exponentielles : ces fonctions ont une courbe représentative qui est une courbe exponentielle, avec une croissance exponentielle ou décroissance exponentielle. La forme de la courbe dépend du coefficient de la fonction.

Exemple de fonction linéaire : y = 2^x

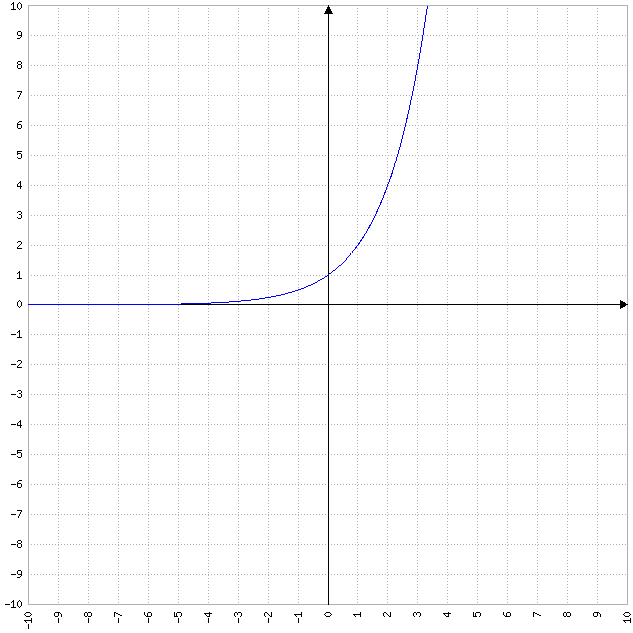
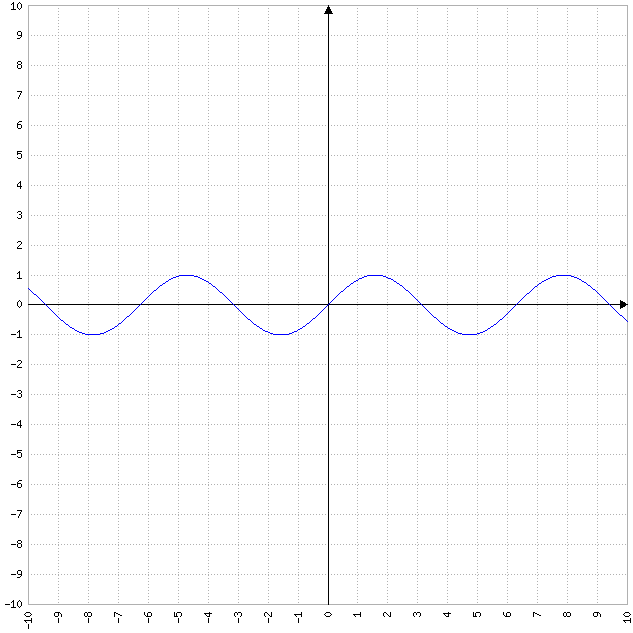
• Les fonctions trigonométriques : ces fonctions ont une courbe représentative qui est une courbe sinusoïdale, avec une périodicité et une amplitude qui dépendent des coefficients de la fonction. Les fonctions trigonométriques peuvent être sinusoïdales, cosinusoïdales, tangentes, cotangentes, etc.

Exemple de fonction linéaire : y = sin(x)

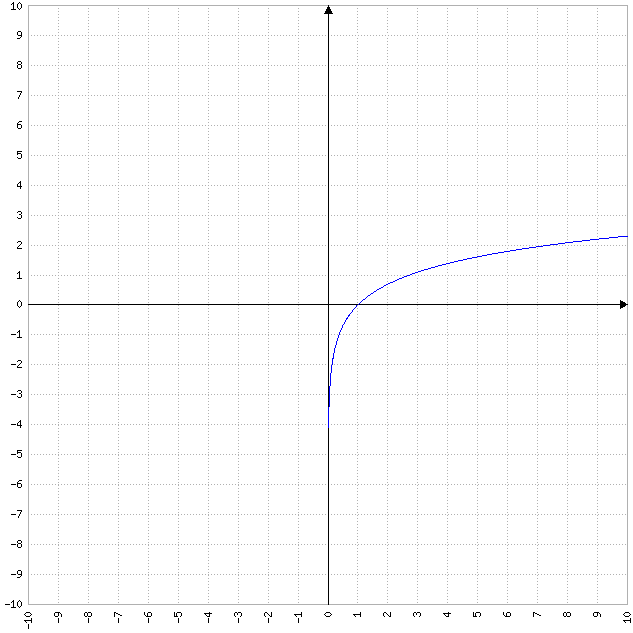
• Les fonctions logarithmiques : ces fonctions ont une courbe représentative qui est une courbe logarithmique, avec une croissance logarithmique ou décroissance logarithmique. La forme de la courbe dépend du coefficient de la fonction.

Exemple de fonction linéaire : y = ln(x)

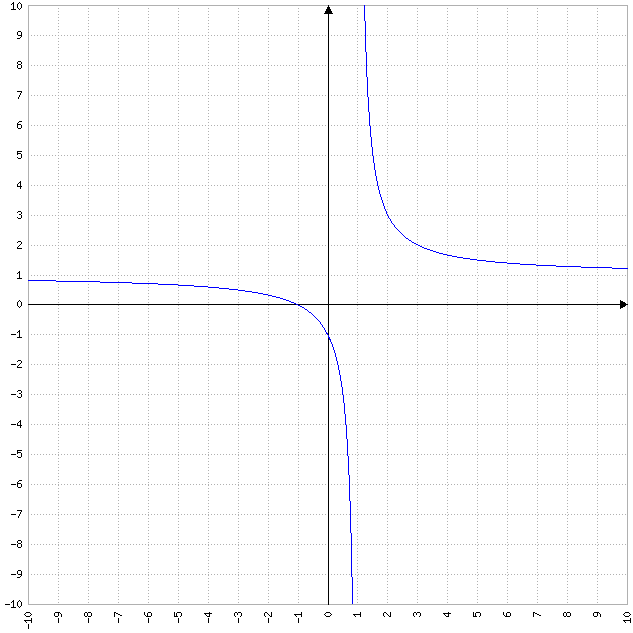
• Les fonctions rationnelles : ces fonctions ont une courbe représentative qui est une courbe rationnelle, qui peut avoir des asymptotes verticales ou horizontales, des points d’inflexion, etc.

Exemple de fonction linéaire : y = (x+1)/(x-1)

Il est important de noter que la forme de la courbe dépend des propriétés de la fonction, telles que sa parité, sa périodicité, sa continuité, etc. Il est donc important de bien comprendre ces propriétés avant de tracer le graphique d’une fonction et d’interpréter la courbe obtenue.

Partie 3 : Domaine et image des fonctions

Définition du domaine et de l’image d’une fonction

Le domaine d’une fonction est l’ensemble de toutes les valeurs d’entrée pour lesquelles la fonction est définie. En d’autres termes, c’est l’ensemble de toutes les valeurs de x pour lesquelles la fonction donne une valeur de y correspondante. Le domaine peut être déterminé en examinant les restrictions de la fonction, telles que les valeurs de x qui rendent le dénominateur d’une fonction rationnelle égal à zéro, ou les valeurs de x pour lesquelles une fonction est définie de manière implicite.

L’image d’une fonction est l’ensemble de toutes les valeurs de sortie possibles pour la fonction. En d’autres termes, c’est l’ensemble de toutes les valeurs de y que la fonction peut prendre. L’image peut être déterminée en examinant le comportement de la fonction pour différentes valeurs d’entrée ou en utilisant les propriétés algébriques de la fonction pour trouver les valeurs maximales et minimales possibles de y.

Il est important de noter que le domaine et l’image peuvent être restreints par les contraintes imposées par le type de fonction, telles que les asymptotes verticales pour les fonctions rationnelles ou les limites inférieure et supérieure pour les fonctions exponentielles. En outre, le domaine et l’image peuvent être affectés par la façon dont la fonction est définie, telles que les fonctions définies par parties qui peuvent avoir des restrictions différentes pour chaque partie.

Comment trouver le domaine et l’image d’une fonction

Pour trouver le domaine d’une fonction, vous devez d’abord rechercher toutes les restrictions à laquelle la fonction est soumise. Par exemple, pour une fonction rationnelle, vous devez exclure les valeurs de x qui rendent le dénominateur égal à zéro, car ces valeurs rendraient la fonction indéfinie. Pour les fonctions radicales, vous devez vous assurer que l’expression sous la racine carrée est positive ou nulle, sinon la fonction serait également indéfinie.

Une fois que vous avez déterminé les restrictions, le domaine sera l’ensemble de toutes les valeurs de x qui ne sont pas soumises à ces restrictions.

Pour trouver l’image d’une fonction, vous pouvez utiliser différentes méthodes en fonction du type de fonction. Pour les fonctions linéaires, vous pouvez déterminer l’image en examinant la pente et l’ordonnée à l’origine de la droite. Pour les fonctions quadratiques, vous pouvez trouver l’image en déterminant le sommet de la parabole et en utilisant la valeur y correspondante. Pour les fonctions exponentielles, l’image sera l’ensemble de toutes les valeurs positives, car l’exponentielle est une fonction croissante qui tend vers l’infini lorsque x tend vers l’infini.

En général, pour trouver l’image d’une fonction, vous pouvez examiner les propriétés de la fonction, tels que sa concavité, sa monotonie, et ses limites. Vous pouvez également utiliser des outils de calcul tels que les dérivées pour trouver les extréma locaux et les points d’inflexion de la fonction, qui peuvent vous aider à déterminer l’image.

Importance du domaine et de l’image dans la compréhension des fonctions

Le domaine et l’image sont deux concepts fondamentaux pour comprendre le comportement d’une fonction. Le domaine définit les valeurs de l’ensemble de départ (le domaine de définition) pour lesquelles la fonction est définie, tandis que l’image est l’ensemble des valeurs que la fonction prend lorsque x varie dans le domaine.

Connaître le domaine d’une fonction est important pour déterminer quelles valeurs de x peuvent être utilisées comme entrée pour la fonction. Si vous utilisez une valeur en dehors du domaine, la fonction ne sera pas définie et vous obtiendrez une erreur. De plus, la connaissance du domaine peut aider à comprendre les restrictions que la fonction impose sur les valeurs de x.

La compréhension de l’image d’une fonction est également importante, car elle donne une idée de l’étendue de la fonction. Les valeurs de l’image peuvent être utilisées pour déterminer les valeurs les plus hautes et les plus basses de la fonction, ce qui peut être important pour l’analyse de la fonction. De plus, la connaissance de l’image peut aider à comprendre la façon dont les valeurs de x sont transformées en valeurs de y, et peut être utile pour trouver les extrêmes de la fonction.

En résumé, le domaine et l’image sont des concepts clés dans l’étude des fonctions, car ils permettent de déterminer les restrictions et l’étendue de la fonction. Ils sont donc essentiels pour comprendre le comportement de la fonction et pour l’utiliser correctement dans des applications pratiques.

Conclusion :

Récapitulation des points clés de l’article

Cet article traite des fonctions mathématiques et fournit une compréhension complète de ce concept fondamental. Voici les points clés qui ont été abordés :

• Les fonctions sont des relations entre deux ensembles de nombres, qui assignent une unique valeur de sortie pour chaque valeur d’entrée.
• Les fonctions peuvent être de différents types, tels que linéaires, quadratiques, exponentielles, etc. Chaque type a une forme et un comportement spécifiques.
• Les fonctions sont généralement notées sous forme d’équations, où x représente la variable d’entrée et f(x) représente la variable de sortie.
• La représentation graphique d’une fonction est un moyen visuel de représenter les valeurs d’entrée et de sortie de la fonction, et permet de mieux comprendre son comportement. Le graphique peut être obtenu en traçant les points (x, f(x)) sur un système de coordonnées.
• Le domaine de définition est l’ensemble des valeurs d’entrée pour lesquelles la fonction est définie, tandis que l’image est l’ensemble des valeurs de sortie que la fonction peut prendre. Ces concepts sont importants pour comprendre les restrictions et l’étendue de la fonction.
• Pour trouver le domaine et l’image d’une fonction, il faut comprendre les restrictions sur les valeurs d’entrée et de sortie, ainsi que le comportement de la fonction.
• Les fonctions sont importantes dans les mathématiques, mais aussi dans la vie quotidienne, car elles permettent de modéliser des situations réelles et de résoudre des problèmes pratiques.

En comprenant ces points clés, on peut acquérir une compréhension solide des fonctions et de leur utilisation en mathématiques et dans la vie de tous les jours.

Réaffirmation de l’importance des fonctions dans les mathématiques et dans la vie quotidienne

Les fonctions sont un concept fondamental en mathématiques, qui sont utilisées dans de nombreuses disciplines, telles que la physique, l’économie, la biologie, la chimie, etc. Elles permettent de modéliser des phénomènes réels de manière abstraite et de résoudre des problèmes complexes.

Dans les mathématiques pures, les fonctions sont étudiées pour leur comportement et leurs propriétés, et elles sont utilisées pour décrire des relations entre des ensembles de nombres. En algèbre, par exemple, les fonctions sont utilisées pour résoudre des équations et pour représenter des relations linéaires et non-linéaires.

Dans la vie quotidienne, les fonctions sont utilisées pour modéliser des phénomènes tels que la croissance d’une population, le mouvement d’un objet, la propagation d’une maladie, la consommation d’énergie, etc. Les fonctions permettent de prédire les résultats futurs en fonction des données actuelles, ce qui est important pour la prise de décision.

En conclusion, les fonctions sont un concept important en mathématiques et dans la vie quotidienne, et leur compréhension est essentielle pour la résolution de problèmes pratiques. Que ce soit en tant que base de la modélisation ou de l’analyse de données, les fonctions sont un outil puissant pour comprendre et expliquer les phénomènes dans le monde qui nous entoure.

Incitation à continuer à explorer les fonctions pour approfondir ses connaissances en mathématiques.

L’étude des fonctions est une discipline passionnante en mathématiques, qui permet de comprendre et de modéliser de nombreux phénomènes dans le monde. Il est donc important de continuer à explorer les fonctions pour approfondir ses connaissances en mathématiques.

En étudiant les fonctions, on peut acquérir des compétences et des connaissances qui sont applicables dans de nombreuses disciplines, telles que l’ingénierie, la finance, la physique, la biologie, etc. La maîtrise des fonctions peut également être utile dans la résolution de problèmes complexes, tant en mathématiques pures qu’en applications pratiques.

Il existe de nombreuses ressources en ligne, des livres et des cours qui peuvent aider à approfondir ses connaissances en fonctions. Il est important de continuer à pratiquer et à appliquer ces concepts dans des exercices pratiques pour renforcer sa compréhension et sa maîtrise de la matière.

En conclusion, l’étude des fonctions est essentielle pour développer une compréhension approfondie des mathématiques et de leur application dans le monde réel. En continuant à explorer les fonctions, on peut acquérir des compétences et des connaissances qui peuvent être utiles dans de nombreux domaines professionnels et académiques.