Comme je vous l’avais précisé dans un article précédent, nous pouvons dans le prolongement de la construction de la droite d’Euler, construire le cercle d’Euler de Feuerbach, Karl Wilhelm (1800-1834) – Mathématicien allemand, pour cela nous pouvons reprendre la précédente construction.
Il suffit de construire les points suivants :
- les milieux des côtés du triangle
- les pieds des hauteurs
- les milieux des segments reliant les sommets à l’orthocentre
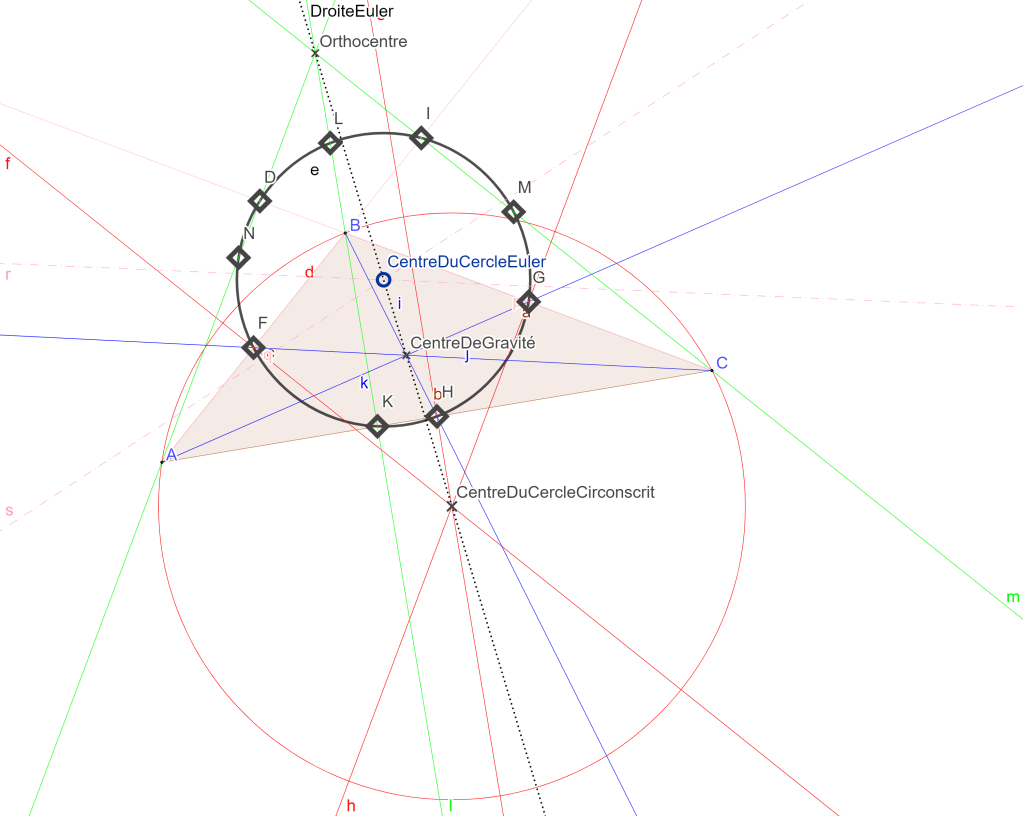
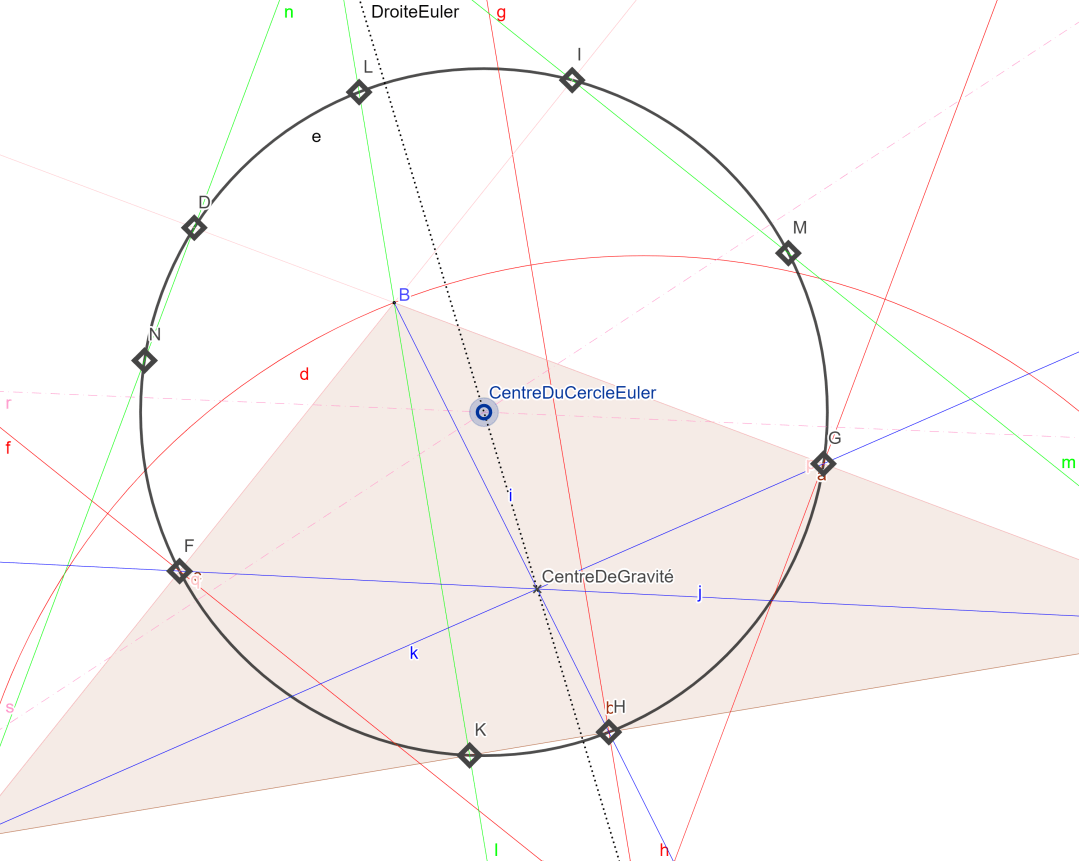
Ainsi nous pouvons constater que ces neufs points appartiennent à la circonférence d’un même cercle appelé cercle d’Euler.
Mais comment tracer un cercle alors que nous n’avons pas de centre ?
Il suffit simplement de tracer deux cordes. Mais qu’est-ce qu’une corde ?
En géométrie, une corde est un segment reliant deux points d’un cercle ou d’une autre courbe.
Puis comme vous savez tracer des médiatrices, il suffit de tracer les médiatrices de ces deux cordes. Le point d’intersection entre ces deux médiatrices vous donnera alors le centre du cercle d’Euler qu’il sera possible de construire ! 😊
Abonnez-vous pour y accéder
Découvrez la suite de ce contenu dès aujourd’hui en vous abonnant.

Un commentaire sur « À la découverte de la construction du cercle de Feuerbach, Karl Wilhelm (1800-1834) – Mathématicien allemand. »